

第2讲 力与直线运动
考点一 匀变速直线运动规律及应用
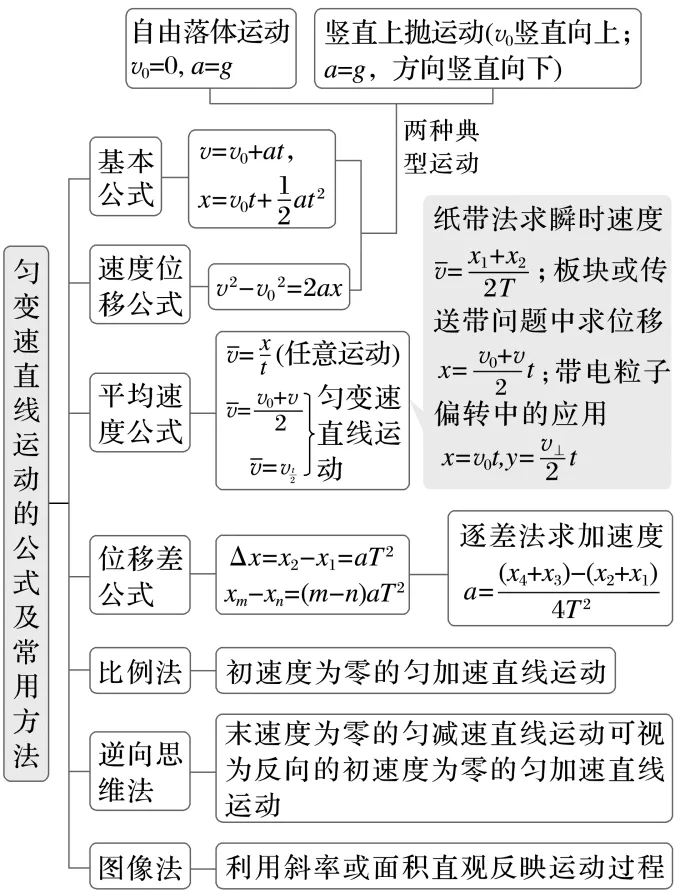
例1 (2025·安徽卷·4)汽车由静止开始沿直线从甲站开往乙站,先做加速度大小为a的匀加速运动,位移大小为x;接着在t时间内做匀速运动;最后做加速度大小也为a的匀减速运动,到达乙站时速度恰好为0。已知甲、乙两站之间的距离为8x,则( )
A.x=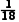 at2B.x=
at2B.x=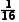 at2
at2
C.x=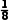 at2D.x=
at2D.x=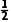 at2
at2
答案 A
解析设匀加速直线运动时间为t',匀速运动的速度为v,有x=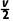 t',根据逆向思维,可知匀减速直线运动阶段的位移等于匀加速直线运动阶段的位移,则匀速直线运动阶段有8x-x-x=vt,联立解得t'=
t',根据逆向思维,可知匀减速直线运动阶段的位移等于匀加速直线运动阶段的位移,则匀速直线运动阶段有8x-x-x=vt,联立解得t'=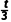 ,根据x=
,根据x=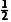 at'2,解得x=
at'2,解得x=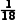 at2,A正确,B、C、D错误。
at2,A正确,B、C、D错误。
例2 (2024·广西卷·13)如图,轮滑训练场沿直线等间距地摆放着若干个定位锥筒,锥筒间距d=0.9 m,某同学穿着轮滑鞋向右匀减速滑行。现测出他从1号锥筒运动到2号锥筒用时t1=0.4 s,从2号锥筒运动到3号锥筒用时t2=0.5 s。求该同学:

(1)滑行的加速度大小;
(2)最远能经过几号锥筒。
答案 (1)1 m/s2 (2)4
解析(1)根据匀变速运动规律,某段内的平均速度等于中间时刻的瞬时速度,可知在1、2间中间时刻的速度为v1=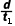 =2.25m/s
=2.25m/s
2、3间中间时刻的速度为v2=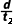 =1.8m/s
=1.8m/s
故可得加速度大小为
a=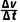 =
=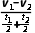 =1m/s2
=1m/s2
(2)设到达1号锥筒时的速度为v0,根据匀变速直线运动规律得v1=v0-a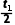
代入数据解得v0=2.45m/s
从1号开始到停止时通过的位移大小为x=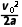 =3.00125m≈3.33d
=3.00125m≈3.33d
故可知最远能经过4号锥筒。
考点二 牛顿运动定律的应用
1.牛顿第二定律
(1)表达式:F=ma,其中F为物体所受的合外力,F、m、a三个量对应同一个物体,且各量都取国际单位。
(2)应用常用方法:
①矢量合成法:若物体只受两个力作用,可用平行四边形定则求这两个力的合力,合力的方向与加速度的方向相同。
②正交分解法:当物体受多个力作用时
常用正交分解法列方程:Fx=ma,Fy=0或Fx=0,Fy=ma
特殊情况下可分解加速度: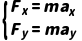
2.系统牛顿第二定律
若研究对象是两个或两个以上的物体,且加速度不同。
系统牛顿第二定律的表达式:
一般形式:∑F外=m1a1+m2a2+m3a3+…
分量形式: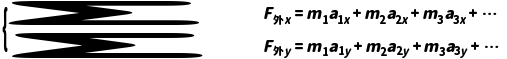
说明:上述表达式左边只有系统受到的外力,内力不需要考虑。
例3 (多选)(2025·安徽卷·5改编)如图,装有轻质光滑定滑轮的长方体木箱静置在水平地面上,木箱上的物块甲通过不可伸长的水平轻绳绕过定滑轮与物块乙相连。乙拉着甲从静止开始运动,木箱始终保持静止。已知甲、乙质量均为1.0 kg,木箱质量为5.0 kg,甲与木箱之间的动摩擦因数为0.5,不计空气阻力,重力加速度g取10 m/s2,则在乙下落的过程中( )
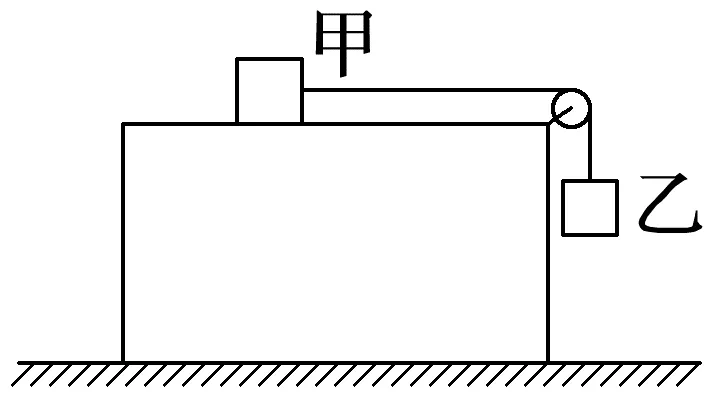
A.甲对木箱的摩擦力方向向左
B.甲运动的加速度大小为2.5 m/s2
C.乙受到绳子的拉力大小为5.0 N
D.地面对木箱的支持力大小为67.5 N
答案 BD
解析根据相对运动,物块甲相对木箱向右运动,甲受到木箱向左的摩擦力,则甲对木箱的摩擦力方向向右,A错误;设物块乙运动的加速度为a,绳子的弹力大小为FT,对甲受力分析有FT-μm甲g=m甲a,对乙受力分析有m乙g-FT=m乙a,联立解得a=2.5m/s2,FT=7.5N,B正确,C错误;只有乙有竖直向下的恒定加速度,对甲、乙和木箱组成的系统,在竖直方向由牛顿第二定律有(M+m甲+m乙)g-FN=m乙a得,FN=(M+m甲+m乙)g-m乙a=67.5N,D正确。
变式(2025·山东日照市二模)如图所示,倾角θ=37°的斜面固定在水平地面上,质量m1=3 kg的物体A置于斜面上,一条轻绳绕过两个光滑的轻质滑轮连接着固定点O和物体A,质量m2=8 kg的物体B与动滑轮连接。已知连接动滑轮两边的轻绳均竖直,物体A与定滑轮间的轻绳和斜面平行,物体A与斜面间的动摩擦因数μ=0.5,最大静摩擦力等于滑动摩擦力,重力加速度g取10 m/s2。初始时物体B的下表面距地面的高度h=2 m,物体A到定滑轮的距离足够远。现将两个物体同时由静止释放,B落地后不反弹。sin 37°=0.6,cos 37°=0.8。
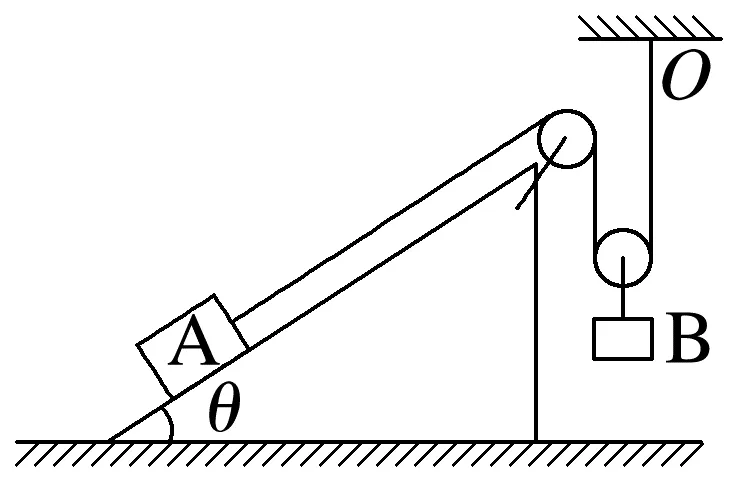
(1)在物体B下落过程中,求轻绳的拉力大小和物体A的加速度大小;
(2)求物体B落地前瞬间的速度大小;
(3)求整个过程中物体A沿着斜面向上运动的最大距离。
答案 (1)36 N 2 m/s2 (2)2 m/s (3)4.8 m
解析(1)对物体A,根据牛顿第二定律F-m1gsinθ-μm1gcosθ=m1a
设物体B的加速度为a1,根据运动关系可知a1=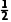 a
a
对物体B,根据牛顿第二定律m2g-2F=m2a1
联立可得拉力大小为F=36N
加速度为a=2m/s2
(2)由运动学公式,有v2=2a1h
可得物体B落地前瞬间的速度大小v=2m/s
(3)物体B从静止释放到落地经历的时间t=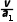 =2s,则物体B落地时,物体A的速度vA=at=4m/s
=2s,则物体B落地时,物体A的速度vA=at=4m/s
B落地后,设A的加速度大小为a2
由牛顿第二定律有m1gsinθ+μm1gcosθ=m1a2
B落地后,根据运动学公式0-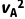 =-2a2s1
=-2a2s1
物体A沿着斜面向上运动的最大距离s=2h+s1
代入数据解得s=4.8m。

四类常见连接体问题
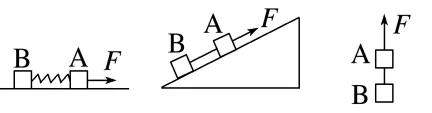
接触面光滑,或μA=μB | 三种情况中弹簧弹力、绳的张力大小相同且与接触面是否光滑无关 |
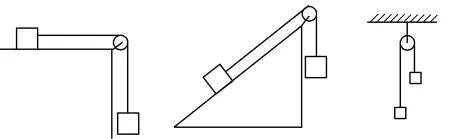
跨滑轮的连接体 | 两物体速度和加速度大小相同、方向不同,常用隔离法 |
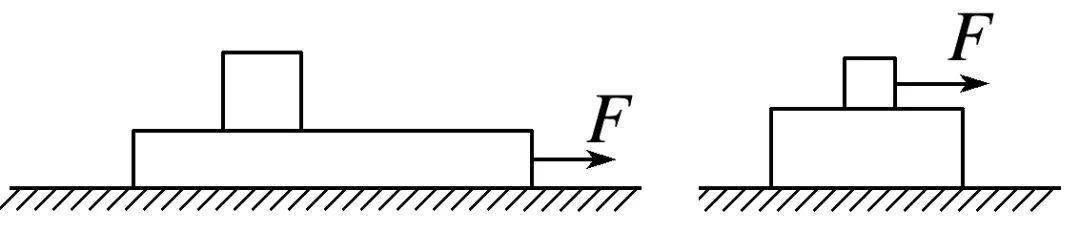
叠加类连接体 | 两物体刚要发生相对滑动时物体间达到最大静摩擦力 |
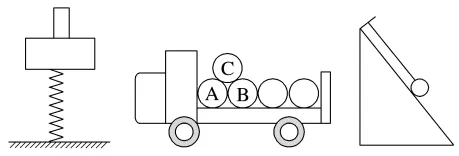
靠在一起的连接体 | 分离时相互作用力为零,但此时两物体的加速度仍相等 |
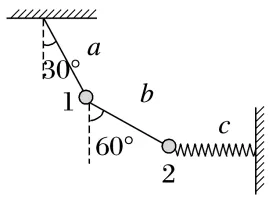
例4 (2025·湖南浏阳市校联盟联考)如图所示,用轻绳a、b和弹簧c将小球1与小球2悬挂在空中,轻绳a与竖直方向夹角为30°,轻绳b与竖直方向夹角为60°,弹簧c水平。小球1的质量为m,重力加速度大小为g。下列说法正确的是( )
A.弹簧c的拉力为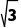 mg
mg
B.小球2的质量为2m
C.剪断轻绳b的瞬间,小球1的加速度大小为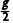
D.剪断轻绳b的瞬间,小球2的加速度方向竖直向下
答案 C
解析对小球1进行受力分析,如图甲
根据平衡条件有FTasin30°=FTbsin60°,FTacos30°=mg+FTbcos60°,
解得FTa=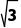 mg,FTb=mg
mg,FTb=mg
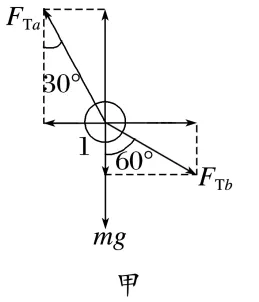
对小球2进行受力分析,如图乙
根据平衡条件有FTc=FTbsin60°,m2g=FTbcos60°
解得FTc=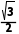 mg,m2=
mg,m2=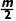 ,故A、B错误;
,故A、B错误;
剪断轻绳b的瞬间,小球1受重力和绳a的拉力,小球1将做圆周运动,受力分析如图丙
根据牛顿第二定律,有mgsin30°=ma1,解得a1=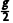 ,故C正确;
,故C正确;
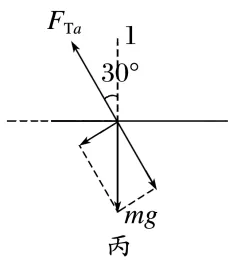
剪断轻绳b的瞬间,小球2受重力和弹簧弹力作用,受力分析如图丁,
根据牛顿第二定律,有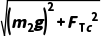 =m2a2,解得a2=2g
=m2a2,解得a2=2g
设加速度的方向与水平方向成α角,有tanα=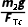 =
=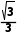 可得α=30°,加速度方向与水平方向成30°角,故D错误。
可得α=30°,加速度方向与水平方向成30°角,故D错误。
例5 (2025·福建福州市模拟)滑雪是我国东北地区冬季常见的体育运动。如图(a),在与水平面夹角θ=14.5°的滑雪道上,质量m=60 kg的滑雪者先采用两滑雪板平行的滑雪姿势(此时雪面对滑雪板的阻力可忽略),由静止开始沿直线匀加速下滑x1=45 m;之后采取两滑雪板间呈一定角度的滑雪姿势,通过滑雪板推雪获得阻力,匀减速继续下滑x2=15 m后停止。已知sin 14.5°=0.25,sin 37°=0.6,重力加速度g取10 m/s2,不计空气阻力。
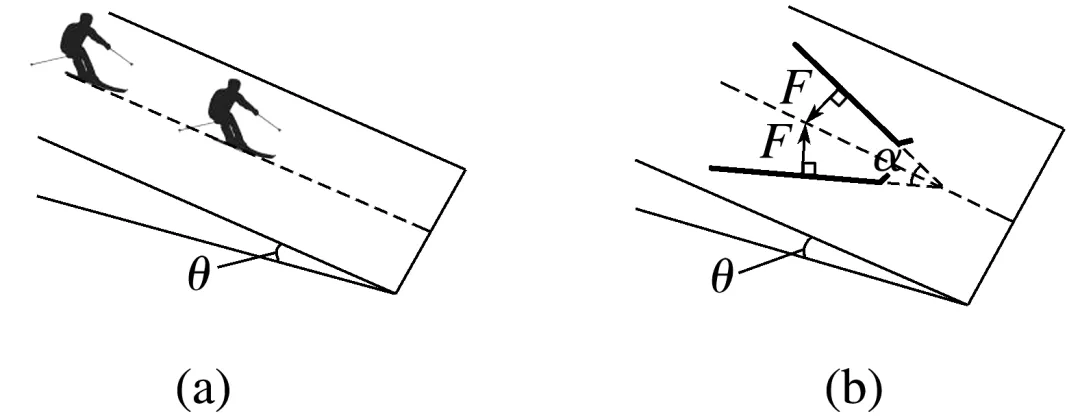
(1)求减速过程中滑雪者加速度a的大小;
(2)如图(b),若减速过程中两滑雪板间的夹角α=74°,滑雪板受到沿雪面且垂直于滑雪板边缘的阻力均为F,求F的大小。
答案 (1)7.5 m/s2 (2)500 N
解析(1)由静止开始沿直线匀加速下滑的过程有2a1x1=v2
由牛顿第二定律知mgsinθ=ma1
代入数据得v=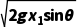 =15m/s
=15m/s
匀减速继续下滑的过程有2ax2=v2
代入数据得a=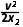 =7.5m/s2
=7.5m/s2
(2)若减速过程中两滑雪板间的夹角α=74°,根据牛顿第二定律有2Fsin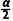 -mgsinθ=ma
-mgsinθ=ma
解得F=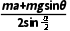 =500N。
=500N。

解决动力学两类基本问题的思路
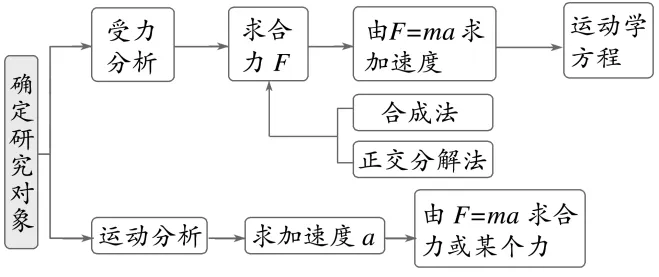
考点三 运动学和动力学图像
1.三种运动学图像

通过网盘分享的文件:2026版物理步步高大二轮专题复习【培优版】
链接: https://pan.baidu.com/s/1IqYFt52DO9gGcuCIcSPR_g?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享