


一、带电粒子在组合场中的运动
1.带电粒子的“电偏转”和“磁偏转”的比较
| 磁偏转 | 电偏转 |
情景图 | 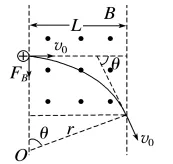
垂直进入磁场 | 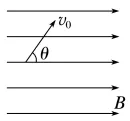
进入磁场时速度与磁场有一定夹角 | 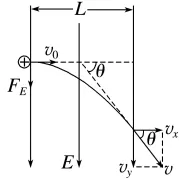
垂直进入电场 | 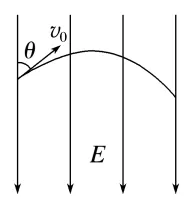
进入电场时速度方向与电场有一定夹角 |
受力 | FB=qv0B,FB大小不变,方向变化,方向总指向圆心,FB为变力 | F=qv0Bsin θ | FE=qE,FE大小、方向均不变,FE为恒力 |
运动规律 | 匀速圆周运动 r=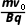 = =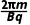 | 螺旋式运动qv⊥B=m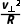 螺距x=v0cos θ·t | 类平抛运动 vx=v0,vy=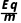 t t x=v0t,y=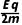 t2 t2 | 类斜抛运动 vx=v0sin θ,vy=v0cos θ-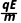 t t x=v0sin θ·t,y=v0cos θ·t-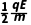 t2 t2 |
2.常见运动及处理方法
例1 (2025·河南卷·15)如图,水平虚线上方区域有垂直于纸面向外的匀强磁场,下方区域有竖直向上的匀强电场。质量为m、带电荷量为q(q>0)的粒子从磁场中的a点以速度v0向右水平发射,当粒子进入电场时其速度沿右下方向并与水平虚线的夹角为60°,然后粒子又射出电场重新进入磁场并通过右侧b点,通过b点时其速度方向水平向右。a、b到水平虚线的距离均为h,两点之间的距离为s=3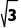 h。不计重力。
h。不计重力。
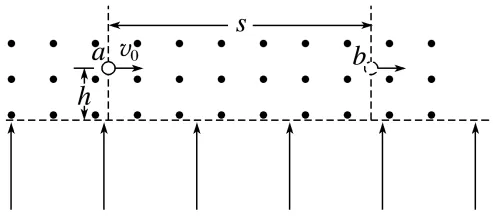
(1)求磁感应强度的大小;
(2)求电场强度的大小;
(3)若粒子从a点以v0竖直向下发射,长时间来看,粒子将向左或向右漂移,求漂移速度大小。(一个周期内粒子的位移与周期的比值为漂移速度)
答案 (1)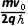 (2)
(2)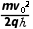 (3)
(3)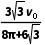
解析(1)根据题意可知,画出粒子的运动轨迹,如图甲所示
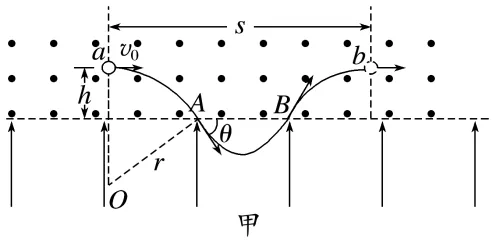
由题意可知θ=60°
设粒子在磁场中做圆周运动的半径为r,由几何关系有r=rcosθ+h
解得r=2h
由牛顿第二定律有qv0B=m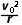
解得B=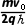
(2)根据题意,由对称性可知,粒子射出电场时,速度大小仍为v0,方向与水平虚线的夹角为60°,由几何关系可得AB=s-2rsinθ=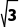 h
h
在电场中,粒子在垂直电场方向做匀速直线运动,则粒子在电场中的运动时间t=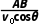 =
=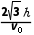
粒子沿电场方向做匀加速直线运动,由牛顿第二定律有qE=ma
由运动学公式有-v0sinθ+at=v0sinθ
联立解得E=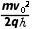
(3)作出粒子在磁场和电场中运动的部分轨迹,如图乙所示
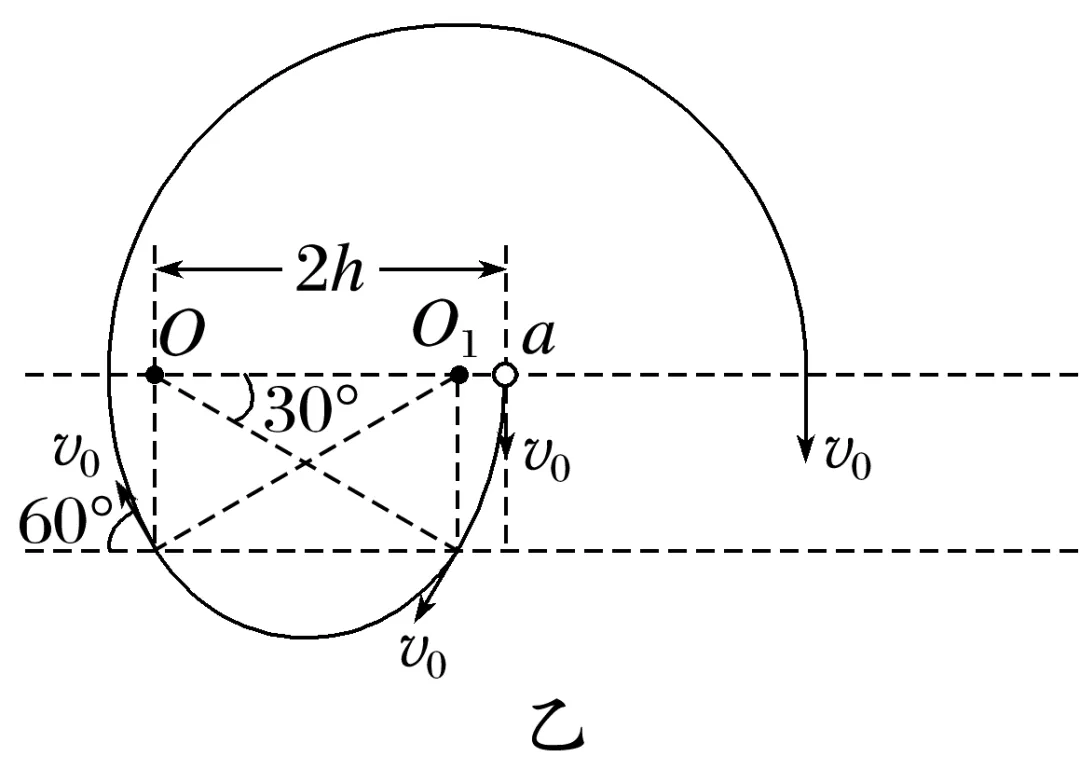
设粒子在磁场中做匀速圆周运动的周期为T,粒子在磁场、电场中的运动具有周期性,在一个实际运动的周期T'内,粒子在磁场中运动的时间
t1=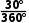 T+
T+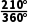 T=
T=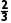 T①
T①
T=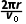 =
=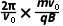 =
=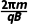 ②
②
联立①②解得t1=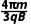
将B=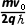 代入可得t1=
代入可得t1=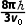
粒子在电场中运动一次的时间t2满足
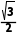 v0=
v0=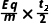
将E=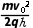 代入可得t2=
代入可得t2=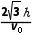
根据图乙中的几何关系可知,一个周期内粒子运动的位移(以向右为正方向)x=OO1=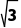 h
h
说明经过一个周期后粒子运动到初始位置右侧,则漂移速度大小v=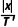 =
= =
=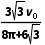 。
。

“5步”突破带电粒子在组合场中的运动问题

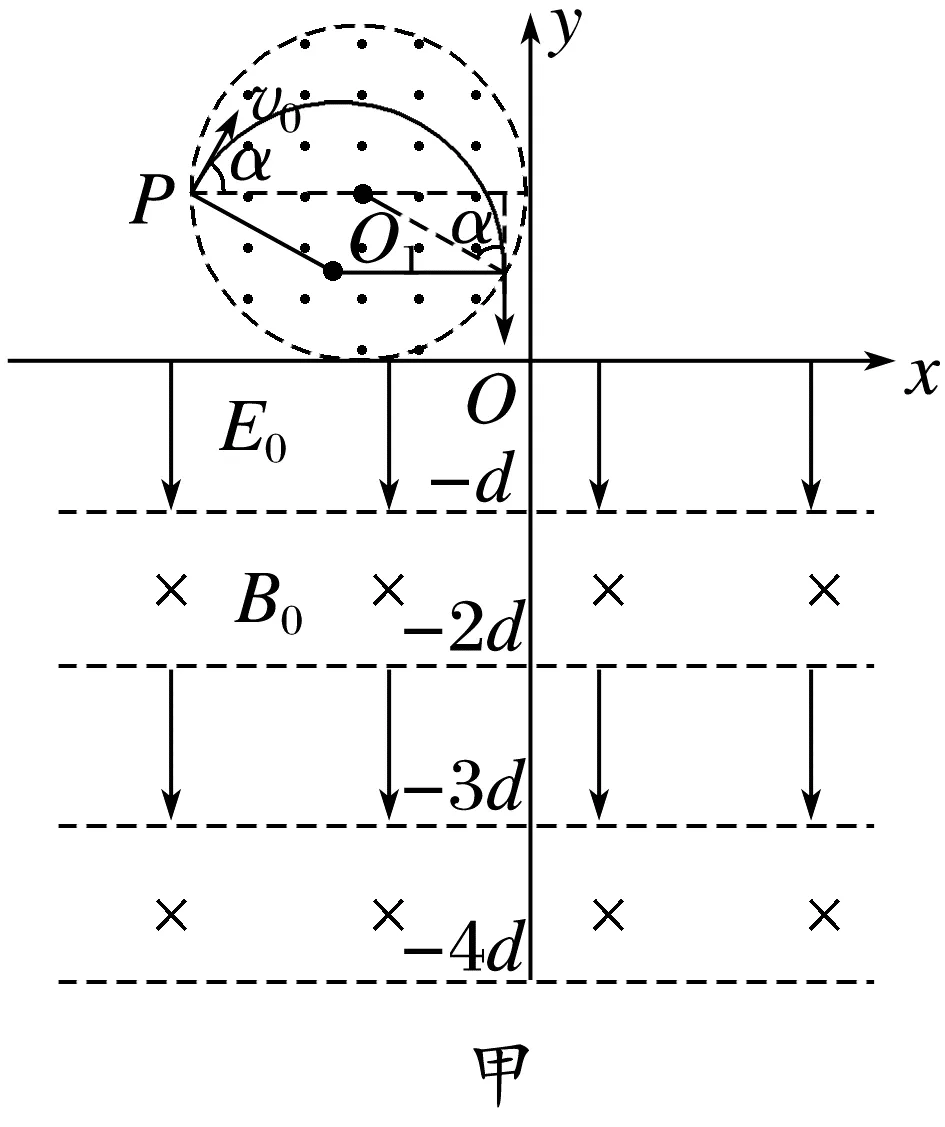
例2 (2025·山东青岛市一检)如图所示,xOy平面直角坐标系中,在第二象限内存在垂直纸面向外的圆形匀强磁场区域,O1为圆心,半径为R,磁场边界与两坐标轴相切;y≤0区域内交替分布宽度均为d的匀强电场和匀强磁场,其边界均与x轴平行,匀强电场的电场强度大小为E0,方向沿y轴负方向,匀强磁场的磁感应强度大小为B0,方向垂直于纸面向里。一质量为m、电荷量为+q的带电粒子,从圆形边界上的P点以初速度v0射入磁场,PO1与x轴平行,v0与PO1夹角α=60°。粒子射出圆形磁场瞬间,在y>0区域内加上沿y轴正方向的匀强电场(图中未画出)。已知圆形磁场的磁感应强度大小为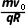 >0区域内匀强电场的电场强度大小为
>0区域内匀强电场的电场强度大小为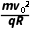 ,不计粒子重力。
,不计粒子重力。
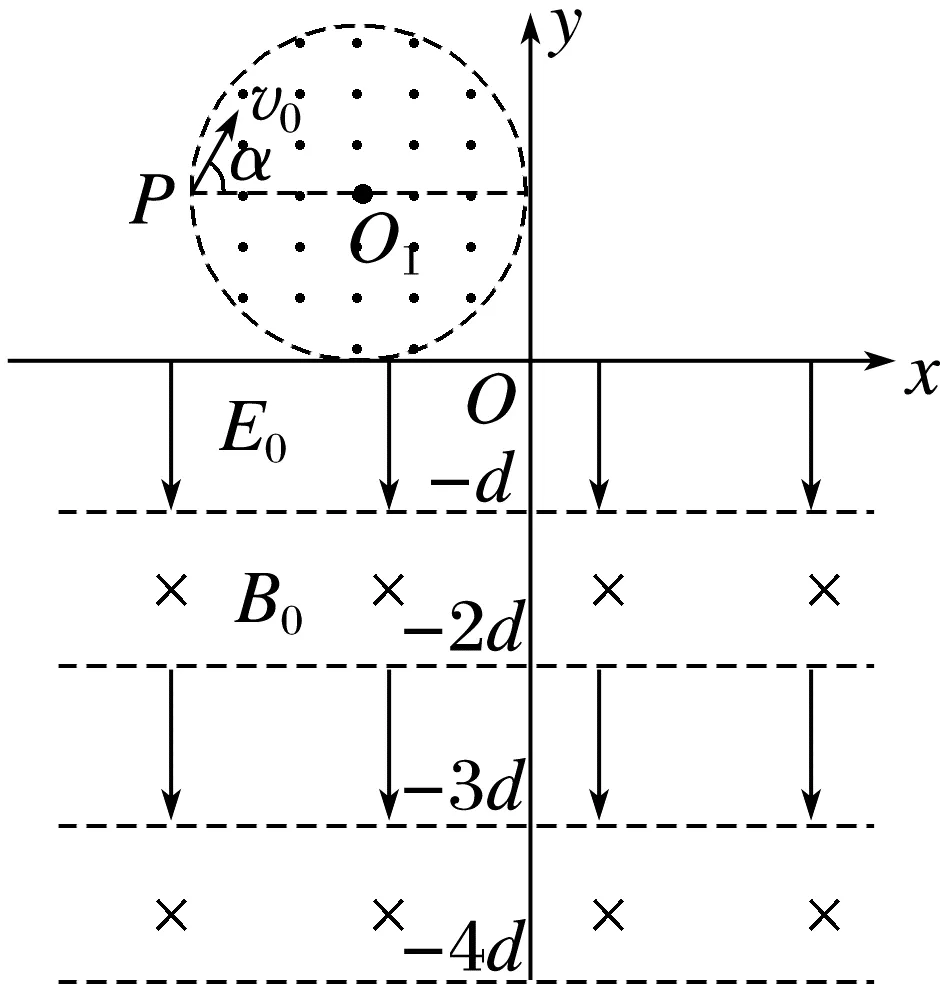
(1)求粒子在圆形磁场区域做圆周运动的半径;
(2)求粒子离开圆形磁场区域后,到达x轴的速度大小;
(3)求粒子穿出y≤0区域内第二个电场时速度方向与竖直方向夹角的正弦值;
(4)若粒子到达y≤0区域内某个磁场下边界时,速度方向恰好沿x轴正方向,求此时速度大小。
答案 (1)R (2)0 (3)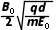 (4)
(4)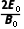
解析(1)粒子在第二象限圆形磁场中,
有qv0B1=m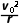
其中B1=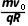
解得r=R
(2)如图甲所示
由几何关系得粒子射出圆形磁场时距离x轴d1=R(1-cosα)
粒子从射出圆形磁场到x轴,由动能定理得-qE1d1=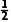 mv2-
mv2-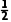 m
m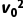
解得v=0
(3)粒子在y≤0区域第一个电场中加速,由动能定理得qE0d=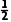 m
m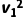
粒子在y≤0区域第一个磁场中,有qv1B0=m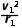
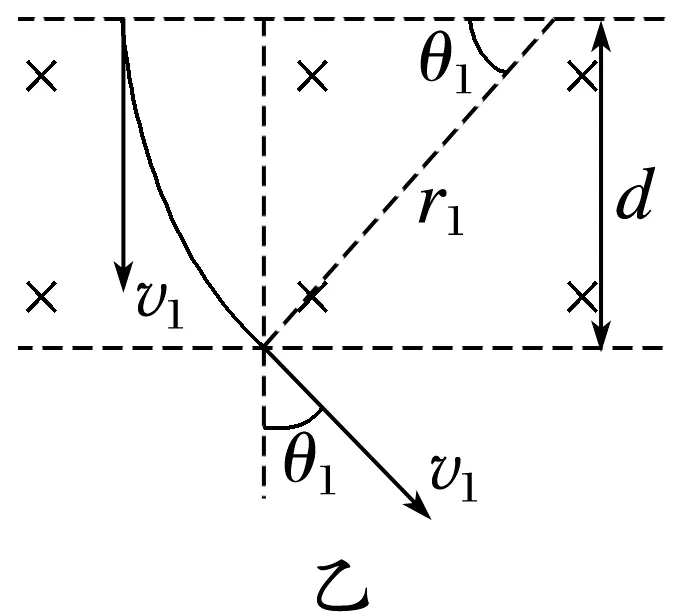
如图乙所示
由几何关系得r1sinθ1=d
粒子在y≤0区域经历两个电场加速,有2qE0d=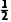 m
m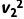 1sinθ1=v2sinθ2
1sinθ1=v2sinθ2
解得sinθ2=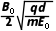
(4)设粒子在第n个磁场下边界的速度为vn,粒子在y≤0区域整个向下运动过程中,由动能定理得nqE0d=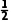 m
m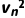
水平方向由动量定理得q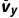 B0t=mvn
B0t=mvn
其中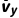 t=nd
t=nd
解得vn=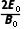

正则动量定理的应用
利用动量定理即洛伦兹力的冲量等于速度的动量变化,把粒子某一方向的位移和垂直该方向的速度变化联系起来。具体用法如下:
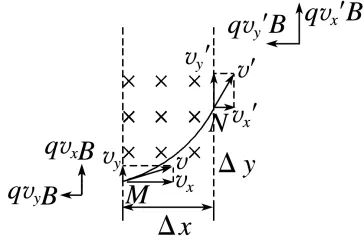
①Ix=m(vx'-vx)=mΔvx=-∑qBvyΔt=-qBΔy或-qBΔy=mΔvx
②Iy=m(vy'-vy)=mΔvy=∑qvxBΔt=qBΔx
qBΔx=mΔvy
二、带电粒子在立体空间中的运动
带电粒子在立体空间中的运动问题,往往通过降维思想进行简化,常见示例及解题策略如下表:
运动类型 | 解题策略 |
在三维坐标系中运动,每个轴方向都是常见运动模型 | 将粒子的运动分解为三个方向的运动 |
一维加一面,如螺旋式运动 | 螺旋式运动:将粒子的运动分解为一个轴方向的匀速直线运动或匀变速直线运动和垂直该轴所在面内的匀速圆周运动 |
运动所在平面切换,粒子进入下一区域偏转后运动轨迹曲线不在原来的平面内 | 把粒子运动所在的面隔离出来,转换视图角度,把立体图转化为平面图,分析粒子在每个面的运动 |
例3 (2024·湖南卷·14)如图,有一内半径为2r、长为L的圆筒,左右端面圆心O'、O处各开有一小孔。以O为坐标原点,取O'O方向为x轴正方向建立xyz坐标系。在筒内x≤0区域有一匀强磁场,磁感应强度大小为B,方向沿x轴正方向;筒外x≥0区域有一匀强电场,场强大小为E,方向沿y轴正方向。一电子枪在O'处向圆筒内多个方向发射电子,电子初速度方向均在xOy平面内,且在x轴正方向的分速度大小均为v0。已知电子的质量为m、电量为e,设电子始终未与筒壁碰撞,不计电子之间的相互作用及电子的重力。
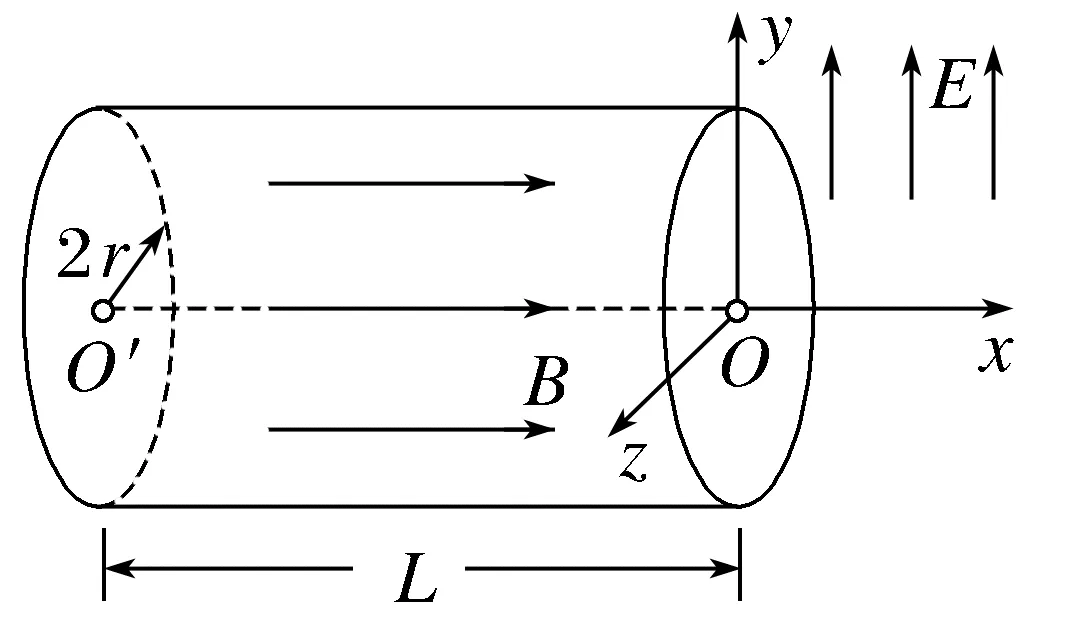
(1)若所有电子均能经过O进入电场,求磁感应强度B的最小值;
(2)取(1)问中最小的磁感应强度B,若进入磁场中电子的速度方向与x轴正方向最大夹角为θ,求tan θ的绝对值;
(3)取(1)问中最小的磁感应强度B,求电子在电场中运动时y轴正方向的最大位移。
答案 (1)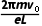 (2)
(2)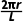 (3)
(3)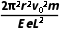
解析(1)电子在匀强磁场中运动时,将其分解为沿x轴的匀速直线运动和在yOz平面内的匀速圆周运动,设电子入射时沿y轴的分速度大小为vy,由电子在x轴方向做匀速直线运动得L=v0t
在yOz平面内,设电子做匀速圆周运动的半径为R,周期为T,
由牛顿第二定律知Bevy=m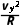
可得R=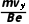 =
=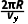 =
=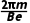
若所有电子均能经过O进入电场,

通过网盘分享的文件:2026版物理步步高大二轮专题复习【培优版】
链接: https://pan.baidu.com/s/1IqYFt52DO9gGcuCIcSPR_g?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享