

计算题培优练7 电磁感应中的综合问题
[训练1]
[分值:28分]
1.(12分)(2025·四川攀枝花市三模)如图所示,一个匝数n=1 000、面积S=100 cm2的水平圆形线圈内有竖直向上的匀强磁场B1,磁感应强度大小随时间变化关系为B1=B0+0.25t。线圈与右侧的平行导轨MN、M'N'通过开关K相连,导轨MN、M'N'构成的平面为水平面,其内有竖直向下的匀强磁场B2,其右侧有倾角θ=30°的倾斜平行导轨PQ、P'Q',N与P、N'与P'通过一小段(长度不计)绝缘圆弧平滑连接,PP'、NN'连线均与所有导轨垂直。倾斜平行导轨PQ、P'Q'内有与两导轨构成斜面垂直向下的匀强磁场B3,其顶端Q与Q'之间接有定值电阻R。现有一长L=0.5 m的导体棒ab垂直于导轨静止放置在水平导轨上,与导轨接触良好。闭合开关K后,导体棒由静止开始运动,到达水平导轨右端前已经匀速。已知导轨间距均为L、阻值均不计,导体棒ab、线圈、定值电阻的阻值均相同,导体棒ab的质量m=0.1 kg,匀强磁场B2、B3的磁感应强度大小均为1 T,重力加速度g取10 m/s2,不计一切摩擦,求:
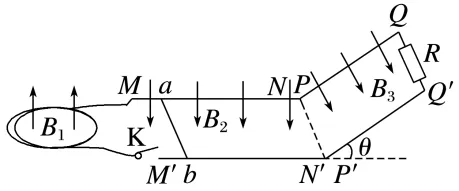
(1)(3分)闭合开关前线圈产生的感应电动势E;
(2)(5分)从闭合开关到导体棒第一次运动到NN'的过程中,导体棒产生的焦耳热Q1;
(3)(4分)若导体棒第一次冲上倾斜导轨经过时间t=1.7 s后又返回导轨底端,求这段时间内导体棒产生的焦耳热Q2。
答案 (1)2.5 V (2)0.625 J (3)0.318 75 J
解析(1)对圆形线圈,由法拉第电磁感应定律有E=n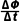 =n
=n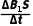
其中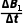 =0.25
=0.25
代入数据得E=2.5V
(2)导体棒ab在到达NN'前已匀速,设匀速时的速度为v1,则有E1=B2Lv1=E
解得v1=5m/s
对导体棒ab从开关闭合到匀速,取水平向右为正方向,由动量定理有B2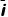 LΔt=mv1-0
LΔt=mv1-0
设这段时间内通过导体棒的电荷量为q,有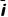 Δt=q
Δt=q
圆形线圈、导体棒ab的电阻相同,由能量守恒定律有E能=Eq=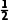 m
m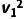 +2Q1
+2Q1
解得Q1=0.625J
(3)从导体棒ab冲上斜面到再次返回斜面底端,全程通过回路的电荷量为零,可得全程安培力的冲量为零。设导体棒返回斜面底端时的速度为v2,取沿斜面向上为正方向,由动量定理,有-mgtsinθ=mv2-mv1
解得v2=-3.5m/s
导体棒ab和定值电阻R的阻值相同,在该过程中,由能量守恒有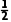 m
m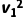 -
-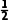 m
m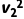 =2Q2
=2Q2
解得Q2=0.31875J。
2.(16分)(2025·海南卷)间距为L的金属导轨倾斜部分光滑,水平部分粗糙且平滑相接,导轨上方接有电源和开关,倾斜导轨与水平面夹角θ=30°,处于垂直于导轨平面向上的匀强磁场中,水平导轨处于竖直向下的匀强磁场中,磁感应强度大小均为B,两相同导体棒ab、cd与水平导轨的动摩擦因数μ=0.25,最大静摩擦力等于滑动摩擦力,两棒质量均为m,接入电路中的电阻均为R,cd棒仅在水平导轨上运动,两导体棒在运动过程中始终与导轨垂直并接触良好,且不互相碰撞,忽略金属导轨的电阻,重力加速度为g。
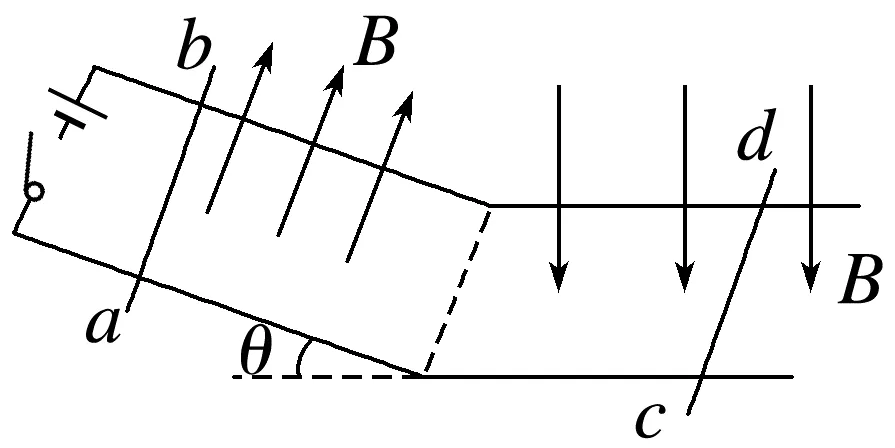
(1)(5分)锁定水平导轨上的cd棒,闭合开关,ab棒静止在倾斜导轨上,求通过ab棒的电流;断开开关,同时解除cd棒的锁定,当ab棒下滑距离为x0时,cd棒开始运动,求cd棒从解除锁定到开始运动过程中,cd棒产生的焦耳热;
(2)(4分)此后ab棒在下滑过程中,电流达到稳定,求此时ab、cd棒的速度大小之差;
(3)(7分)ab棒中电流稳定之后继续下滑,从ab棒到达水平导轨开始计时,t1时刻cd棒速度为零,加速度不为零,此后某时刻,cd棒的加速度为零,速度不为零,求从t1时刻到某时刻,ab、cd的路程之差。
答案 (1)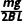
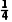 mgx0-
mgx0-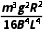 (2)
(2)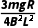 (3)
(3)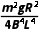
解析(1)ab棒静止在倾斜导轨上,根据平衡条件可得F安=mgsin30°,F安ab=BIabL
解得通过ab棒的电流为Iab=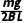
设当ab棒下滑距离为x0时速度为v0,cd棒开始运动时回路中的电流为I1,此时对cd棒有F安cd=μmg
同时有F安cd=BI1L,I1=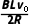
分析可知cd棒从解除锁定到开始运动过程中,cd棒产生的焦耳热与ab棒产生的焦耳热相等,整个过程根据能量守恒可得mgx0sin30°-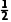 m
m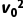 =2Qcd
=2Qcd
联立解得cd棒产生的焦耳热为
Qcd=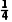 mgx0-
mgx0-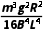
(2)分析可知ab棒在下滑过程中产生的感应电动势与cd棒在向左运动的过程中产生的感应电动势方向相反,故当电流达到稳定时,两棒的速度差恒定,故可知此时两棒的加速度相等,由于两棒受到的安培力大小相等,对两棒有mgsin30°-F安=ma,F安-μmg=ma
同时有F安=BIL,I=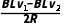 =
=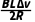
联立解得此时ab、cd棒的速度大小之差为Δv=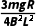
(3)分析可知从开始到t1时刻,两棒整体所受的合外力为零,故该过程系统动量守恒,设t1时刻ab棒的速度为v1',可知mΔv=mv1'
解得v1'=Δv=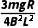
设某时刻时,ab棒速度为v1″,cd棒速度为vcd,cd棒的加速度为零,可得F安cd1=μmg①
其中F安cd1=BI2L
分析可知此时两导体棒产生的电动势方向相反,可得I2=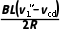 ②
②
从t1时刻到某时刻,对两棒分别根据动量定理有
-(μmg+B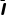 L)Δt=mv1″-mv1',(B
L)Δt=mv1″-mv1',(B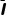 L-μmg)Δt=mvcd
L-μmg)Δt=mvcd
由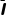 Δt=q可得μmgΔt+BLq=mv1'-mv1″,BLq-μmgΔt=mvcd
Δt=q可得μmgΔt+BLq=mv1'-mv1″,BLq-μmgΔt=mvcd
两式相加得2BLq=mv1'-m(v1″-vcd)③
同时有q=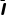 Δt=
Δt=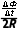 ·Δt=
·Δt=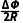 =
=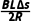 ④
④
联立①②③④可得从t1到某时刻,ab、cd的路程之差为Δs=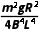 。
。
[训练2]
[分值:27分]
1.(12分)(2025·四川成都市二模)如图所示,将电阻为R=0.02 Ω、质量为m=0.01 kg的单匝正方形闭合线圈abcd水平放置在顺时针运行的水平传送带的最左端,其边长为l=0.1 m,边界MN、PQ与传送带运行方向垂直,在MN、PQ区域内加一个垂直于传送带平面向下、磁感应强度为B=0.4 T的匀强磁场,MN、PQ边界间距为d=0.26 m,线圈在运动过程中左右两边始终与磁场边界平行,其与传送带间的动摩擦因数为μ=0.2,线圈ab边进入磁场区域前已和传送带共速,传送带的速度为v0=1 m/s,t=0时刻,线圈ab边与MN重合,t1=0.2 s时刻,线圈cd边与MN重合,t2时刻线圈ab边与PQ重合,已知重力加速度g取10 m/s2,最大静摩擦力等于滑动摩擦力,求:
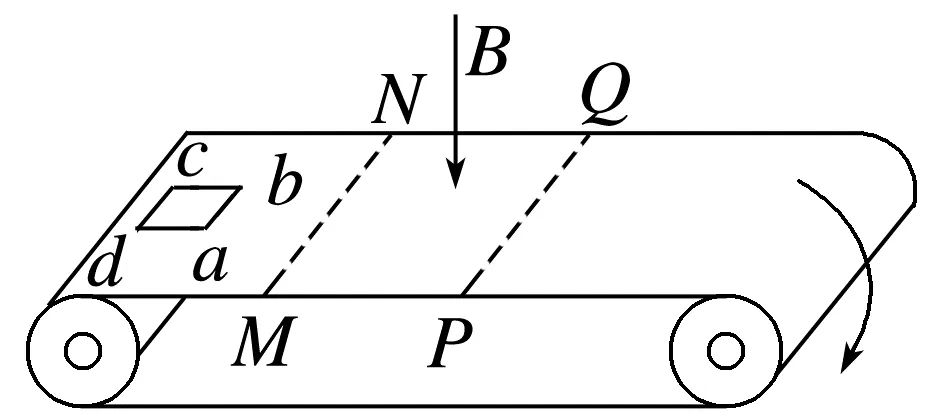
(1)(2分)t=0时刻,线圈中的感应电流大小;
(2)(3分)t1时刻,线圈的速度大小;
(3)(4分)t2;
(4)(3分)0~t2时间内,线圈中产生的焦耳热。
答案 (1)2 A (2)0.6 m/s (3)0.4 s (4)0.005 2 J
解析(1)t=0时刻,线圈中的感应电动势为E=Blv0,线圈中的感应电流大小为I=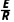
解得I=2A
(2)t1时刻,设线圈的速度大小为v,对线圈进入磁场的过程,以水平向右为正方向,
由动量定理有-B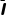 lt1+μmgt1=mv-mv0
lt1+μmgt1=mv-mv0
又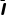 =
=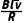 =
=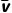 t1
t1
联立解得v=0.6m/s
(3)t1时刻开始,线圈在摩擦力作用下做匀加速直线运动,由牛顿第二定律有μmg=ma
解得a=2m/s2
根据速度时间公式有t加=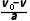 =0.2s
=0.2s
根据速度位移公式有x加=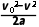 =0.16m
=0.16m
又d=l+x加=0.26m
即线圈与传送带共速时,ab边恰与PQ重合,则有t2=t1+t加
解得t2=0.4s
(4)t1~t2时间内,线圈中焦耳热为0;对线圈,0~t1时间内,根据动能定理有WA+μmgl=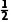 mv2-
mv2-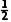 m
m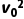
又Q=-WA
解得Q=0.0052J。
2.(15分)(2025·河北卷·15)某电磁助推装置设计如图,超级电容器经调控系统为电路提供1 000 A的恒定电流,水平固定的平行长直导轨处于垂直水平面的匀强磁场中,a可视为始终垂直导轨的导体棒,b为表面绝缘的无人机。初始时a静止于MM'处,b静止于a右侧某处。现将开关S接1端,a与b正碰后锁定并一起运动,损失动能全部储存为弹性势能。当a运行至NN'时将S接2端,同时解除锁定,所储势能瞬间全部转化为动能,a与b分离。已知电容器电容C为10 F,导轨间距为0.5 m,磁感应强度大小为1 T,MM'到NN'的距离为5 m,a、b质量分别为2 kg、8 kg,a在导轨间的电阻为0.01 Ω。碰撞、分离时间极短,各部分始终接触良好,不计导轨电阻、摩擦和储能耗损,忽略电流对磁场的影响。
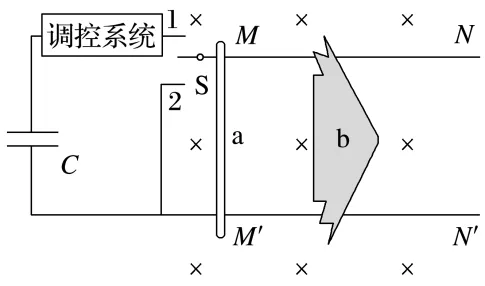
(1)(2分)若分离后某时刻a的速度大小为10 m/s,求此时通过a的电流大小。
(2)(8分)忽略a、b所受空气阻力,当a与b的初始间距为1.25 m时,求b分离后的速度大小,分析其是否为b能够获得的最大速度;并求a运动过程中电容器的电压减小量。
(3)(5分)忽略a所受空气阻力,若b所受空气阻力大小与其速度v的关系为f=kv2(k=0.025 N·s2/m2),初始位置与(2)问一致,试估算a运行至NN'时。a分离前的速度大小能否达到(2)问中分离前速度的99%,并给出结论。(0.992=0.9801)
答案 (1)500 A (2)25 m/s 是 40 V (3)能
解析(1)分离后a切割磁感线有E=BLv
则通过a的电流I=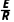
解得I=500A。
(2)由于超级电容器经调控系统为电路提供I0=1000A的恒定电流,则当a与b的初始间距为1.25m时a与b碰撞前的速度设为va,根据动能定理有BI0Lxab=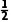 ma
ma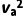
a与b碰撞时根据动量守恒和能量守恒有mava=(ma+mb)v共,ma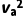 =
=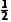 (ma+mb)
(ma+mb)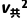 +Ep
+Ep
a与b整体从碰后到NN'的过程中有BI0L(xMN-xab)=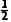 (ma+mb)
(ma+mb)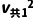 -
-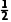 (ma+mb)
(ma+mb)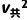
a与b分离时根据动量守恒和能量守恒有(ma+mb)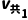 =ma
=ma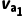 +mb
+mb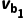 (ma+mb)
(ma+mb)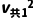 +Ep=
+Ep=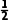 ma
ma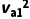 +
+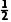 mb
mb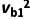
联立解得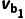 =25m/s,va1=0,此时a速度为零,安培力做功产生的所有能量都转化为b的动能,因此b能获得的最大速度为25m/s。
=25m/s,va1=0,此时a速度为零,安培力做功产生的所有能量都转化为b的动能,因此b能获得的最大速度为25m/s。
由于a和ab组合体均做匀变速直线运动,分别有xab=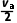 t1,xMN-xab=
t1,xMN-xab=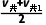 t2
t2
解得t1=0.1s,t2=0.3s,则电容器流出的电荷量有Δq=I0(t1+t2)
a运动过程中电容器的电压减小量ΔU=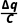 =40V
=40V
(3)从a、b碰后一起运动到NN'过程,由于b受空气阻力,故末速度必小于v共1,故该过程中始终有f<k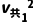 ,如果b所受阻力大小取fm=k
,如果b所受阻力大小取fm=k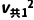 =10N,由动能定理得(BI0L-k
=10N,由动能定理得(BI0L-k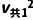 )(xMN-xab)=
)(xMN-xab)=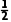 (ma+mb)
(ma+mb)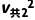 -
-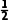 (ma+mb)
(ma+mb)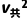
解得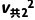 =392.5m2/s2
=392.5m2/s2
由于(0.99v共1)2=0.9801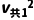 =392.04<
=392.04<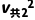 ,故能达到(2)问中分离前速度的99%。
,故能达到(2)问中分离前速度的99%。

通过网盘分享的文件:2026版物理步步高大二轮专题复习【培优版】
链接: https://pan.baidu.com/s/1IqYFt52DO9gGcuCIcSPR_g?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享